Stàtica strutural
 |
Vos an lenga piemontèisa |
| Për amprende a dovré 'l sistema dle parlà locaj ch'a varda sì. |
|
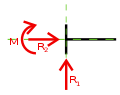
La stàtica strutural a l’é la part dla mecànica ch’a dësvlupa lë studi stàtich dij còrp fìsich ch’as conòsso ant la mecànica strutural, dont trav, tle e retìcoj. Lòn ch'a anteressa ëd pi për la stàtica strutural a l’é lë studi dle struture isostàtiche, përchè mach ant le struture isostàtiche as peul studiè ëd fasson completa sòj posson e soe flession anterne dovrand le condission d’echilibri. Sto studi ancheuj a l’é fàit për la pì part da na mira analìtica e numérica. Na vira as costumava arzòlvlo ëd fasson gràfica, ma al dì d’ancheuj l’arzolussion gràfica a l’é dovrà mach për fé djë spiegon ëscolàstich. Condission d’echilibri strutural[modìfica | modifiché la sorgiss]Na strutura configurà ant na certa manera geométrica a l’é an echilibri se tuti ij sò tòch dëstacàbij a son an echilibri. Ël problema dl’echilibri stàtich ëd na strutura as arzòlv studiand l'echilibri stàtich ëd tùit sòj tòch. A ste relassion d'echilibri a pijo part nen mach le fòrse (e le cobie) aplicà da fòra, ma 'cò ij posson interior che ij tòch a scangio fra 'd lor. Për valuté l'echilibri, ij tòch dla stutura a peulo esse considerà 'me dij còrp rèid.   Equassion fondamentaj dla stàtica[modìfica | modifiché la sorgiss]Na condission necessaria e suficenta për fé sté an echilibri 'n còrp rèid a l'é ch'a sio nule cheidun-e dle quantità an gieugh:
Për un còrp ant lë spassi tridimensional, le doe equassion fondamentaj dla stàtica a ven-o le ses equassion scalar (tre për la traslassion e tre për la rotassion). Ant ël cas pian (le trajetòrie[1] a son part d'un pian, dont ëdcò le fòrse aplicà a son part), j'equassion dla stàtica a corëspondo a tre equassion scalar (doe për la traslassion e un-a për la rotassion dantorn a na diression normal al pian assegnà)[2]. Për un sistema fàit da 'n nùmer qualsëssìa c ëd tòch, dagià che j'equassion dla stàtica a devo valèj për mincadun ëd sòj tòch, ël nùmer dj'equassion a l'é 6c ant ël cas con tre dimension e 3c ant ël cas con doe dimension. Gre ëd libertà[modìfica | modifiché la sorgiss]As ciama gre ëd libertà ël nùmer dij paràmeter cinemàtich ch'a servo për savèj se 'l sistema a bogia (sò moviment) e vàire ch'a bogia (sò andi). Un còrp rèid ant lë spassi tridimensional a l'ha ses gre 'd libertà (tre a traslé e tre a viré). Ant ël problema pian ël còrp rèid a l'ha tre gre 'd libertà (doi a traslé e doi a viré). La cinemàtica d'un sistema fàit da c còrp rèid as conòss an studiand la cinemàtica ëd minca còrp dël sistema. Ij sò gre 'd libertà a son donch la soma dij gre 'd libertà ëd tùit sòj tòch. As peul noté che ël gre ëd libertà d'un sistema a l'é ugual al nùmer d'equassion scalar ch'a venta trové për echilibré ël sistema istess. Condission ëd vìncol[modìfica | modifiché la sorgiss]Un vìncol a l'é lòn ch'a sot-pon a dle condission ël moviment dij còrp. Ij vìncoj as diso estern o assolù s'a condission-o ël sistema antregh, as diso antern s'a condission-o mach ël moviment fra ij tòch dël sistema. As ciama gre ëd vìncol ël nùmer dle componente dël moviment ch'a resto condissionà: con ës significà-sì as parla ëd vìncol sempi se a blòca mach na componenta dël moviment, e peui ëd vìncol dobi, tripl e via fòrt, cand le componente blocà a son pì che un-a. As parla cediment ëd vìncol cand ël vìncol a l'é pì nen bon a anulé la componenta corëspondenta dël moviment. An mecànica clàssica ij vìncoj a son dle fòrse, dagià ch'a modìfico 'l moviment d'un sistema minca vira che 'l sistema a tenta 'd trasgredije. An efet as ciama reassion vincolar la fòrsa che un vìncol a àplica. Për ch'a-i peula essie na reassion vincolar, a venta che ël vìncol a sia compatìbil con le componente dij vetor da bloché: sòn a detèrmina dle caraterìstiche vetoriaj (diression e pont d'aplicassion) dle reassion vincolar, e donch ël nùmer ëd paràmeter scalar independent (ij grè ëd vìncol) ch'a servo a esprime la reassion vincolar. Sòrt ëd vìncoj[modìfica | modifiché la sorgiss]  Ant ij problema dë stàtica pian-a, ij vìncoj pì dovrà a son costi sì-dapress:
Càlcol dij vìncoj[modìfica | modifiché la sorgiss]
La condission d'isostaticità a l'é:
Stuture isostàtiche, iperstàtiche e pericolante[modìfica | modifiché la sorgiss]A 'n livel teòrich as podrìa pijé , ël nùmer d'element, e , ël nùmer ëd vìncoj, e fortì che:
Ste relassion a son vàlide. Tutun a-i son le struture ciamà tralignà ch'a rispeto la condission d'isostaticità, ma che, për colpa dla disposission ëd sòj vìncoj, a son sia iperstàtiche, sia pericolante, e a peulo taché a bogé ëdcò con grand moviment. Le prime doe relassion, sl'iperstaticità e la pericolansa, a son suficente, ma nen necessarie, dagià ch'a esisto dë struture iperstàtiche e pericolante ch'a-j rëspeto nen. La dariera relassion, sl'isostaticità, a l'é necessaria, ma nen suficenta, dagià che ij vìncoj a podrìo esse mal butà e ineficass e la strutura a podrìa bogé istess. A venta donch dimostré nen mach che a l'é ugual a , ma ëdcò che ij vìncoj a gavo dabon tuta possibilità ëd moviment. Le struture isostàtiche a son prevalente an stàtica strutural, dagià ch'as peul arzòlvje univocament an studiand soe reassion vincolar e sòj sfòrs interior, mach an dovrand le condission d'echilibri stàtich. Për sta rason a son ciamà dcò struture staticaman determinà. Për le struture iperstàtiche, nomach j'equassion stàtiche a basto nen pr'arzòlvje: ant ës cas-sì a venta dovré 'l métod ëd le fòrse o 'l métod dle reidure. Le struture pericolante, nopà, as peulo mach identifiché, ma as peul nen arzòlvje da na mira stàtica e dij cit cinematism: a son dë struture dinàmiche. Nòte[modìfica | modifiché la sorgiss]
|