Lej ëd gravitassion universal
 |
Vos an lenga piemontèisa |
| Për amprende a dovré 'l sistema dle parlà locaj ch'a varda sì. |
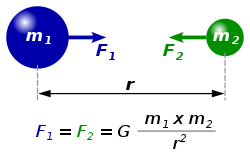 La lej ëd gravitassion universal o lej ëd Newton a fortiss che minca còrp a esèrcita ansima a minca àutr còrp na fòrsa d'atrassion ch'a l'ha tanme diression la reta ch'a gionz ij doi còrp e dont l'antensità a l'é proporsional ëd fasson direta al prodot ëd soe masse e ëd fasson anversa al quadrà dle distanse dij doi còrp:
Costa lej a l'ha smonula Isaac Newton ant ij sò Principia mathematica. Ël valor dla costanta gravitassional G a l'é stàit trovà për prim da Henry Cavendish dël 1798, an dovrand n'angign conossù coma la balansa ëd Cavendish. Na mzura pi precisa a l'é stàita fàita dël 1942 da P.R. Heyl e P. Chizanowski, ch'a l'han otnù ël valor
La dedussion dle masse dij còrp celest[modìfica | modifiché la sorgiss]Da la lej ëd Newton as peulo trovesse ij valor dle masse dij còrp celest. Për esempi, an aprossimand a na sirconferensa ël moviment dantorn al sol d'un pianeta, cost-sì a l'é soget, a tut moment, a l'assion newtonian-a sentrìpeta , anté che M a l'é la massa dël sol, m cola dël pianeta e R a l'é la distansa antra 'l pianeta e ël sol. Ciamà a l'acelerassion sentrìpeta e T l'ann sideral, visadì ël perìod d'arvolussion dël pianeta dantorn al sol, un a oten
dont
|





